平均律 【音律】平均律クラヴィーア ピアノ調律 音階周波数 男性・女性音域平均 倍音ハーモニクス
ピッチを平均して調節するのが平均律で、オクターヴは12音の半音に分割できますが、
これを全て均一の周波数比で構成する十二平均律は、現代で一般的に用いられている音律です。
平均律とは
平均律が登場した歴史は古く、16世紀にはガリレオ・ガリレイが半音を17:18にとる平均律を発見し、実際に利用されていました。この比で与えられる半音は、現代の12音平均律よりごく僅か狭い(18/17の12乗=約1.98556となる)ですが、計算値としての平均律もガリレオ・ガリレイがこの平均律を発見した直後に考案されています。
ミーントーンはある程度自由な転調を可能とした音律でしたが、スムーズに転調できない調もありました。
そこで物理的な音の協和と、音楽としての実用性の両面から考えられた音律が平均律で、オクターヴの12音の半音を同じピッチで平均して調節しています。
現代で一般的に用いられている十二平均律は、このように半音を全て均一の周波数比で構成した音律です。
隣接する2つの音(半音)の周波数比は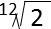 (2の12乗根:約1.0596)となり、協和音程は極めて単純な整数比に近くなりますが、オクターヴ以外に周波数比が単純な整数比になる音程はありません。
(2の12乗根:約1.0596)となり、協和音程は極めて単純な整数比に近くなりますが、オクターヴ以外に周波数比が単純な整数比になる音程はありません。
平均律の最大の利点は、調性による差異がなく転調が容易であることで、自由な転調を可能としました。また楽器による差異を標準化しやすいという利点もあります。
しかし当時は、心地よい音程がオクターヴ以外に存在しないということが欠点とされ、そのため平均律が普及するのは19世紀後半以降になります。
19世紀後半以降では、作曲家の多様な要求に応えうる音律とされ、優れたピアノ曲も多く作曲されています。また第二次産業革命に伴い音楽の分野でも、この時期にはピアノの性能が向上し、ピアノが大量生産されるようになりました。
音程表(セント値)<ピタゴラス音律・純正律・平均律>
| 音程 | ピタゴラス音律 | 平均律 | 純正律 |
|---|---|---|---|
| 完全1度 | 0 | 0 | 0 |
| 増1度 | 114 | 100 | 96 |
| 短2度 | 90 | 100 | 133 |
| 長2度 | 204 | 200 | 182or204 |
| 増2度 | 318 | 300 | 275 |
| 短3度 | 294 | 300 | 275 |
| 長3度 | 408 | 400 | 386 |
| 減4度 | 384 | 400 | 427 |
| 増3度 | 522 | 500 | 461 |
| 完全4度 | 498 | 500 | 498 |
| 増4度 | 612 | 600 | 569 |
| 減5度 | 588 | 600 | 631 |
| 完全5度 | 702 | 700 | 702 |
| 増5度 | 816 | 800 | 773 |
| 短6度 | 792 | 800 | 814 |
| 長6度 | 906 | 900 | 884 |
| 増6度 | 1020 | 1000 | 955 |
| 短7度 | 996 | 1000 | 969 |
| 長7度 | 1110 | 1100 | 1088 |
| 減8度 | 1086 | 1100 | 1129 |
| 増7度 | 1223 | 1200 | 1159 |
| 完全8度 | 1200 | 1200 | 1200 |
完全5度はピタゴラス音律と純正律では同じ数値であり、長3度は極端にかけ離れています。
ピタゴラスサークル上で隣り合う半音は90セント、全音は204セントになるだけですので、ピタゴラス音律の数値は容易に作り出すことができます。
主音がCの場合は、短2度(D♭)が主音から90セント、長2度(D)が204セント、短三度(E♭)がDから90セント、長3度(E)がDから204セント・・・というように構成されます。
ピタゴラス音律の五度を積み上げていくと、平均律との誤差(2セント)分が順に広がっていきます。Cから五度を積み上げた場合では、G→D→A→E→H→Fis(増4度)→Cis(増1度)→Gis(増5度)と順に2セントずつ平均律との差は広がり、5度ずつ下がっていく場合には逆に2セントずつ狭まっていきます。

