ピタゴラス音律 【ピタゴラスの定理】ドレミファソラシド音階周波数 ソルフェジオ バイオリンチューニング
音律を初めて体系的に定めたのが、ギリシャのピタゴラスです。
ピタゴラス音律は、完全5度を積み上げた音程を基本とする音律です。
ピタゴラス音律

音律を初めて体系的に定めたのは、「万物の根源は数である」と考えていたギリシャのピタゴラス(紀元前496年頃~582年頃)です。
ピタゴラスはオクターヴに次いで、オクターヴの中で最も調和する音程は完全5度であると考えました。
オクターヴが2/1の比率であるため、この比に次ぐ単純な比が完全5度を作り出すと考え、この音程に周波数比3/2の関係を充当しました。
基本となるC音の完全5度上のG音に、C音の3/2倍の周波数を充当し、さらにG音の完全5度上のD音に、G音の3/2倍の周波数を充当しますが、この場合は初めのC音から1オクターヴを越えてしまいますので、オクターヴ下げて周波数を半分にします。
このような関係からC音とD音の周波数比は、3/2×3/2×1/2=9/8となり、ピタゴラスの音律の長2度(全音)音程の周波数比は9/8となります。E音とF音のような短2度(半音)の周波数比は256/243となります。
このようにして完全5度ずつ上昇させていき、オクターヴを越える場合には周波数を半分にして、各音の周波数を決めていきます。
このピタゴラス音律では、完全5度(3/2)、完全4度(4/3)の音程は単純な周波数比になり、美しい響きが得られますが、長3度音程の周波数比(81/64)などは、複雑な周波数比になるため快い響きが得られません。
しかし、当時の音楽は主声部が一つであるモノフォニーが主流でしたので、この欠点は特に問題にはなりませんでした。
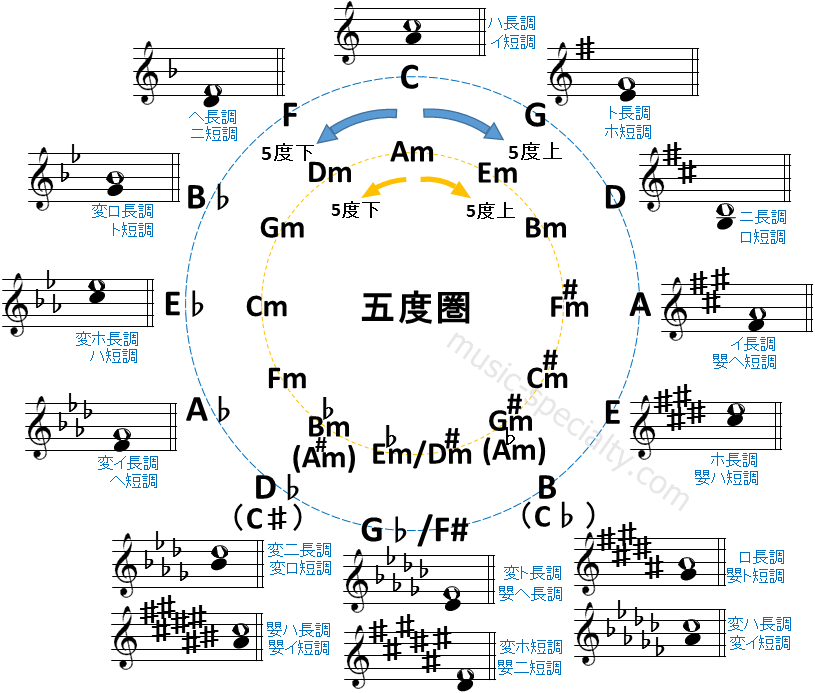
基準になるC音から上下に完全五度ずつ上昇下降していくと、オクターヴ内の半音階上の12音が全て登場して元のC音に戻りますが、この状況を円環で表したものを5度圏といいます。
完全5度を3/2の周波数比で定義し、5度圏上の音の周波数を定めた場合、「FーC」間の音程は同じオクターヴ内に収めると、完全5度よりも少し小さくなってしまいます。
五度圏
ピタゴラス音律と平均律とのセント差比較
※セント
・音律を理論的に表示し分かり易くするために使われる対数値。
※単位換算
・1オクターブ=1200セント
・十二平均律の半音=100セント
・十二平均律の全音=200セント
・ピタゴラス音律の長2度、周波数比9/8(大全音)=約204セント。
※周波数比からセント値計算
・1200*log周波数比/log2
(周波数比の常用対数を2の常用対数で割って1200を掛ける)
| ピタゴラス | 0 | 702 | 204 | 906 | 408 | 1110 | 612 | 114 | 816 | 318 | 1020 | 522 | 24(1224) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 平均律 | 0 | 700 | 200 | 900 | 400 | 1100 | 600 | 100 | 800 | 300 | 1000 | 500 | 0(1200) |
| 上行 | C→ | G→ | D→ | A→ | E→ | H→ | Fis→ | Cis→ | Gis→ | Dis→ | Ais→ | Eis→ | His |
| 下行 | Fes | ←Ces | ←Ges | ←Des | ←As | ←Es | ←B | ←F | ←C | ||||
| 平均律 | 400 | 1100 | 600 | 100 | 800 | 300 | 1000 | 500 | 0 | ||||
| ピタゴラス | 384 | 1086 | 588 | 90 | 792 | 294 | 996 | 498 | 0 |
ピタゴラス音律の5度関係は、平均律と比べて2セント広く、基準から離れていくにつれ平均律からもかけ離れていきます。
完全5度ずつ上昇する度に右方向へ移動し、2セントずつ差が広がり、反対では完全5度ずつ下降する度に左方向へ移動し、2セントずつ下に差が広がります。
異名同音が上下ですべて24セントずれていますが、これがピタゴラス音律を構成する音になります。
このセントは半音の約1/4で約23.46セントの値になり、ピタゴラスコンマやダイトニックコンマと呼ばれます。
ピタゴラスの音楽への影響
(紀元前496年頃~紀元前582年頃)
エーゲ海にあるギリシャのサモス島生まれで、古代ギリシャの数学者であり哲学者。
すべてのアルケー(万物の根源)を「数」と考えました。
紀元前530年頃に、ギリシャの都市クロトンにピタゴラス教団を設立し、ピタゴラスや弟子たちは「ピタゴラス学派」と呼ばれ、彼らは数学の基礎となる数々の定理を発見し、その思想はプラトンを始め後世の哲学者へ大きな影響を与えています。
全ての物事を「数」の原理で考えようとしたピタゴラスは、古代ギリシャにおいて音楽理論の始祖としても位置付けられています。
「音楽教程」という音楽理論書には、ある日ピタゴラスはハンマーの出す音を聴いて、耳に心地よい調和した響きを生むハンマーの組み合わせに気付き、ハンマーの重さのみが音の調和に関わっていることを知り、その後ハンマーの正確な重さを量り、同じ素材で同じより糸から作った4つの弦と重りを使った実験を通して、その重さの違い(比率)から協和する音程の振動数の整数比を算定します。
この数値の発見は「ピタゴラス音律」と呼ばれ、ギリシャ音楽理論の展開の基となり、現在の音階へと受け継がれています。

